Sources

R packages

"ape" (Paradis et al 2004)

"MCMCglmm" (Hadfield, 2010a)

Data

Phenotypic data ("data_simple.txt"), Data frame containing the phenotypic data

Phylogeny ("phylo.nex"), Phylogeny file (NEXUS file)

Codes

We will begin by fitting the simple comparative model described in main text section 11.2.1, using simulated data. Assume we have measurements of a phenotype phen (say the body size) and a cofactor variable (say the temperature of the environment), for several species: 

  library(ape)
  library(MCMCglmm)
  phylo<-read.nexus("phylo.nex")
  data<-read.table("data_simple.txt",header=TRUE)
  head(data)

##     phen cofactor phylo
## 1 107.07   10.310  sp_1
## 2  79.61    9.691  sp_2
## 3 116.38   15.008  sp_3
## 4 143.29   19.088  sp_4
## 5 139.61   15.658  sp_5
## 6  68.51    6.005  sp_6
We want to investigate a possible relationship between the phenotypes and the cofactor, while controlling for any phylogenetic dependency in the dataset. To achieve our goal, we want to use the phylogenetic mixed model implemented in the MCMCglmm package. Note the phylo column containing the name of the species in our dataset: it corresponds to the phylogenetic effect we are going to include in our model. In order to do so, we need to calculate the inverse of the $ \bm{\Sigma}$ matrix of phylogenetic correlation: 
  inv.phylo<-inverseA(phylo,nodes="TIPS",scale=TRUE)
The inverseA() function accepts R phylogenetic objects. Here, we state that we wants to calculate $ \bm{\Sigma}^{-1}$ using the argument nodes=`TIPS'. If, as explained in the Introduction of the main text, we want to calculate the inverse of the bigger matrix $ \bm{\Omega}$ (for a much larger phylogeny, it would be much more efficient), we would have used nodes=`ALL' to include ancestral nodes into the calculation. The scale argument yields a correlation matrix (scaling total branch length, from root to tips, to one).

Now, we have the inverse of our matrix, but because it is using a Bayesian framework, this package needs prior distributions for the fixed and random effects. The default prior for the fixed effects is suitable for our needs. However, regarding the random effects, we need to define a set of priors for the variance components of reach random effect: 

  prior<-list(G=list(G1=list(V=1,nu=0.02)),R=list(V=1,nu=0.02))
These priors (G for the random effect(s), and R for the residual variance) correspond to an inverse-Gamma distribution with shape and scale parameters equal to 0.011, which is relatively canonical, though not without drawbacks (see Gelman, 2006, for more information). The model is then defined as follows: 
model_simple<-MCMCglmm(phen~cofactor,random=~phylo,
  family="gaussian",ginverse=list(phylo=inv.phylo$Ainv),prior=prior,
  data=data,nitt=5000000,burnin=1000,thin=500)
Here, we assume a linear relationship between phen and cofactor, with a random effect phylo corresponding the phylogenetic effect. The argument ginverse allows us to include a custom matrix for our random effect phylo, using the results of the inverseA function (above). We used the prior variable defined above. The variables nitt and burnin are used to calibrate the MCMCM algorithm: it will iterate for burnin iterations before recording samples (to ensure convergence), and then iterate nitt times. The parameter thin helps us to save memory by saving only every `thin' value and thus, dropping highly auto-correlated values2. Note that the use of nodes=`TIPS' or nodes=`ALL' in the inverseA function can have a noticeable impact on auto-correlation: whereas the latter would speed up computation, it can results in higher auto-correlation. Whether to use to one or the other would thus depend mainly on the size of the phylogeny (very large phylogenies would probably need nodes=`ALL' to allow MCMCglmm to run at all). Finally, note that this example can take up to a few hours to run.

After checking for convergence (for example using heidel.diag() function), we can look at the output summary: 

  summary(model_simple)

##  Iterations = 1001:4999501
##  Thinning interval  = 500
##  Sample size  = 9998 
## 
##  DIC: 1516 
## 
##  G-structure:  ~phylo
## 
##       post.mean l-95% CI u-95% CI eff.samp
## phylo       210     92.3      334     9998
## 
##  R-structure:  ~units
## 
##       post.mean l-95% CI u-95% CI eff.samp
## units      85.8     60.8      113    10986
## 
##  Location effects: phen ~ cofactor 
## 
##             post.mean l-95% CI u-95% CI eff.samp  pMCMC    
## (Intercept)     39.71    26.09    53.60     9998 <1e-04 ***
## cofactor         5.18     4.90     5.44     9998 <1e-04 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The first part shows a summary of MCMC sampling parameters, and gives the Deviance Information Criterion (DIC) of the model. The DIC is a model selection criterion comparable to Akaike's Information Criterion (AIC)3. Following are the results for the random effect variances (G-structure, containing the variance of the phylo effect) and the residual variance (R-structure, the residual variance is called units in MCMCglmm). We have information about the posterior mean of the estimate, its 95% credible interval4 and its effective sample size. The latter is a measure of the auto-correlation within the parameter sample: it should be close to the MCMC sample size above, or failing that, it should be at least large enough (say more than 1,000). The summary of the fixed effects (intercept and cofactor) are similar, except we also have a ``pMCMC'' value for significance testing if the parameter is different from zero5. By using plot(model_simple), we can obtain the ``trace'' of the sampling (to check for convergence and auto-correlation) and posterior density of each parameter (Fig. 11.1).
Figure 11.1: Plot of trace and posterior density for fixed effects (top two firsts) and variance parameters (bottom two lasts).

Finally, we can easily calculate the posterior probability of the phylogenetic signal 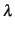$ \lambda$ (see section 11.2.1 in the main text) using: 

lambda <- model_simple$VCV[,'phylo']/
 (model_simple$VCV[,'phylo']+model_simple$VCV[,'units'])
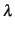
We can calculate the posterior mean (mean of the posterior distribution), posterior mode (most likely value regarding the posterior distribution) and the 95% credible interval of $ \lambda$: 
 mean(lambda)

## [1] 0.6961

 posterior.mode(lambda)

##   var1 
## 0.7442

 HPDinterval(lambda)

##       lower  upper
## var1 0.5267 0.8522
## attr(,"Probability")
## [1] 0.95

Footnotes

... 0.011
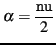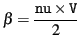MCMCglmm univariate prior formulation is such that it corresponds to an inverse-Gamma with shape parameter $ \alpha=\dfrac{\mathtt{nu}}{2}$ and scale parameter $ \beta=\dfrac{\mathtt{nu}\times\mathtt{V}}{2}$. It is important to note that this inverse-Gamma could become unwantedly `informative' when variance components are close to 0 so that it is always recommended running models with different prior specifications. For which prior should be used, see discussion in Hadfield (2010b) and also one can find more recent discussion on this topic online within the correspondences in the r-sig-mixed-modes mailing list.
... values2
Because the MCMC sampling is Markovian, it is a time-series, which often appears to be auto-correlated: closely following iterations tend to resemble each other. The ``thinning'' help to save memory when running the MCMC for longer. For phylogenetic mixed model, this auto-correlation can be large and problematic: always make sure your effective sample size is large enough and that auto-correlation is low.
... (AIC)3
Here we do not provide explanations on how information criteria can be used for model selection. For a detailed discussion on this topic, the reader is referred to Chapter 12.
... interval4
Credible interval can be considered as the Bayesian version of confidence intervals, and also it is known as the highest posterior density (see Hadfield, 2010b).
... zero5
If we are strictly Bayesian, we should not do significance testing because such a concept belongs to the frequentists' paradigm. However, we use ``pMCMC'' as if frequentists' p-values for convenience.