install.packages("paleotree")
The package and the data can then be loaded with the following two commands:
library(paleotree) data(retiolitinae)
This adds two objects to our workspace in R: a phylogeny (retioTree) and a dataset of stratigraphic ranges (retioRanges). You can always use the function ls() in R to list what objects are in your current workspace. In this case, both retioTree and retioRanges are formatted as "paleotree" would like: retioTree is an unscaled cladogram in the phylo format for the phylogenetic R package "ape" (Paradis et al., 2004); in this case, the consensus tree from Bates et al. (2005). Generally, we can get these trees by reading Newick or NEXUS format files into R using read.tree or read.nexus functions from "ape"; more about the phylo format can be found in the documentation for "ape" (e.g Paradis, 2012). Inputting stratigraphic information, like temporal ranges, can be a little trickier. Let us look at retioRanges a little closer. We can type in the name of an object to print the entire dataset in the console or use the function str to look at the structure of the object:
str(retioRanges)
## List of 2 ## $ int.times :'data.frame': 20 obs. of 2 variables: ## ..$ start_time: num [1:20] 440 439 437 437 436 ... ## ..$ end_time : num [1:20] 439 437 437 436 435 ... ## $ taxon.times:'data.frame': 22 obs. of 2 variables: ## ..$ first_int: int [1:22] 8 6 2 8 8 8 8 13 8 13 ... ## ..$ last_int : int [1:22] 8 10 10 8 14 14 14 14 14 14 ...
At first glance, this may seem complex. For datasets with continuous time appearance dates, all "paleotree" will want is a simple two-column matrix consisting of first and last appearance dates for each taxon, with row names labeled with the taxon names on the cladogram. Most datasets will instead have stratigraphic ranges known only from discrete intervals and thus will require a more complicated structure, like retioRanges. As we can see with str(), retioRanges is actually a list composed of two matrices, each of which are composed of two columns. In R, we can use double square bracket to subset lists and look at each matrix in turn.
retioRanges[[1]]
## start_time end_time ## Coronograptus cyphus 440.2 439.4 ## Demirastrites triangulatus - Demirastrites pectinatus 439.4 437.5 ## Pernerograptus argenteus 437.5 437.0 ## Lituigraptus convolutus 437.0 435.9 ## Stimulograptus sedgwicki 435.9 434.9 ## Spirograptus guerichi 434.9 432.5 ## Spirograptus turriculatus - Stretograptus crispus 432.5 430.4 ## Monoclimacis griestoniensis - Monoclimacis crenulata 430.4 429.4 ## Spirograptus spiralis 429.4 429.0 ## Nanograptus lapworthi - Cyrtograptus insectus 429.0 427.1 ## Crytograptus centhfugus - Cyrtograptus murchisoni 427.1 426.5 ## Monograptus riccartonensis - Monograptus belophorus 426.5 426.1 ## Cyrtograptus rigidus - Cyrtograptus perneri 426.1 424.9 ## Cyrtograptus lundgreni 424.9 424.0 ## Gothograptus nassa - Pristiograptus dubius 424.0 423.1 ## Colonograptus preadeubeli - Colonograptus deubeli 423.1 422.8 ## Colonograptus ludensis 422.8 422.6 ## Neolobograptus nilssoni - Lobograptus progenitor 422.6 422.4 ## Lobograptus scanicus 422.4 421.3 ## Saetograptus leintwardnensis 421.3 420.4
The first matrix (named int.times for interval times), each row is a different interval (i.e. biozone), row names are the names of each interval and the start and end times for the intervals are given in the two columns. Graptolite data like those used in this example are well resolved relative to the data available for many other fossil groups. Some intervals are less than a million years long, all of the occurrences are resolved to a single zone, and none of the zones overlap or contain one another (i.e. they are sequential). Datasets for other groups are often much more complicated than this example. For instance, some datasets may have taxa with bounds on their dates that do not correspond to named intervals. These can be included in the same way.
retioRanges[[2]]
## first_int last_int ## Rotaretiolites 8 8 ## Pseudoplegmatograptus 6 10 ## Pseudoretiolites 2 10 ## Dabashanograptus 8 8 ## Retiolites 8 14 ## Stomatograptus 8 14 ## Paraplectograptus 8 14 ## Pseudoplectograptus 13 14 ## Sokolovograptus 8 14 ## Eisenackograptus 13 14 ## Sagenograptus 14 14 ## Cometograptus 14 14 ## Plectograptus 17 19 ## Plectodinemagraptus 20 20 ## Semiplectograptus 19 20 ## Baculograptus 14 16 ## Doliograptus 15 15 ## Gothograptus 14 16 ## Papiliograptus 16 16 ## Spinograptus 16 17 ## Holoretiolites 18 18 ## Neogothograptus 18 18
The second matrix in retioRanges (named taxon.times for taxon times) only has meaning relative to the first matrix. Here, each row is a taxon, the row names are the taxon labels (which must match the labels on the tree) and the two columns are respectively the interval identifiers for those intervals which that fossil taxon first and last appeared in. The interval identifiers used in these columns reflect the row number for that interval in the matrix of interval start and end dates, i.e. the first matrix of retioRanges. For example, Rotaretiolites first and last appears in the biozone listed on the eighth row (labeled as the Monoclimacis griestoniensis-Monoclimacis crenulata interval).
As this is discrete interval data, we will begin exploring the various time-scaling methods using the bin_timePaleoPhy() function. This function applies the simplest family of time-scaling algorithms, along with an algorithm for randomly resampling appearance dates from within discrete intervals. The simplest of the time-scaling algorithms is the "basic" method, which makes clades as old as their earliest appearing member (Norell, 1992; Smith, 1994). We can easily apply it with:
timetree <- bin_timePaleoPhy(tree = retioTree, timeList = retioRanges, type = "basic", ntrees = 1, plot = TRUE)
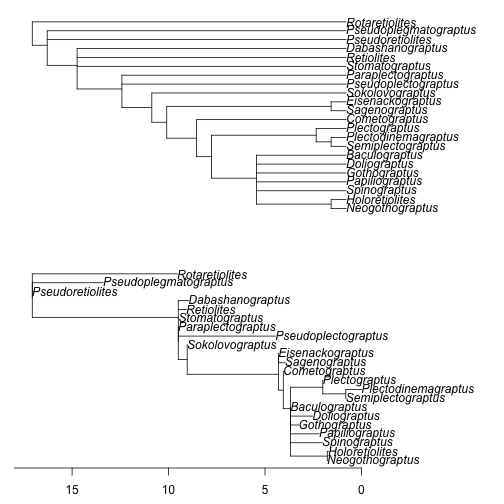
Figure 1. The "basic" method of time-scaling applied to the Retiolitinae dataset taken from Bates et al. (2005). At top the unscaled cladogram used as input is figured, and the lower figure is the time-scaled output. Appearance dates for taxa are randomly resampled from within discrete intervals and polytomies are left unresolved. Times of observation used are the first appearance dates. The time axes shown are not absolute time, but rather counting backwards from the time of the latest tip of the tree, which in this case is Plectodinemagraptus.
The function will immediately issue a warning not to interpret a single output tree, because the dates were randomly resampled. The plotting argument will produce a figure with the cladogram and the time-scaled tree produced (Figure 1). The plots cannot look identical to a user's because they are random (and, for pedagogical purposes, we will avoid using an approach that would remove this disconcerting random element to the tutorial: I want to keep you off balance). The time-axis at the bottom is somewhat misleading, as it assumes the latest tip of the tree is at time 0, which is unfortunate given the latest appearing taxon on the tree is at around 420 million years ago. Thus, the time-axis as plotted only provides dating information relative to this latest tip, although on an absolute scale.
The relative "location" of the tips on the output time-scaled tree reflects the relative first appearance dates of taxa, not their last appearance dates. By default, bin_timePaleoPhy assumes that the times of observation to be used are the first appearance dates, which may not be appropriate for many analyses. Incidentally, this means all the plotted branches represent hypothetical ghost branches and ghost lineages, reflecting unsampled portions of graptoloid evolution history (Norell, 1992; 1993). We can change the times of observation to the last appearance date using the argument add.term:
timetree <- bin_timePaleoPhy(tree = retioTree, timeList = retioRanges, type= "basic", add.term = TRUE, ntrees = 1, plot = TRUE)
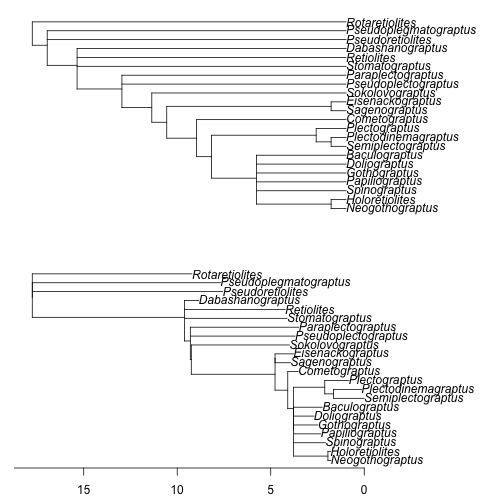
Figure 2. Using last appearance dates as the times of observation can greatly alter the time-scaled branch lengths. As in Figure 1, the top figure is the unscaled cladogram used as input and the lower figure is the time-scaled output, and the axis shown is time relative to the latest terminal tip. Times of observation used are the last appearance dates. Appearance dates for taxa are randomly resampled from within discrete intervals and polytomies are left unresolved.
This argument adds the "terminal" stratigraphic ranges of taxa to the tree. The difference in the choice of times of appearance can greatly alter the tree. For example, the tip with Pseudoretiolites shifts forward in time, because this genus has a long stratigraphic range (Figure 2).
The polytomies in the cladogram have not been resolved in the last two time-scaled phylogenies we have produced. This may exacerbate issues with zero-length branches. To randomly resolve these nodes prior to time-scaling, forcing these trees to be dichotomous, we can use the argument randres which controls the interval application of the function multi2di() from the package "ape".
timetree <- bin_timePaleoPhy(tree = retioTree, timeList = retioRanges, type = "basic", randres = TRUE, add.term = TRUE, ntrees = 1, plot = TRUE)
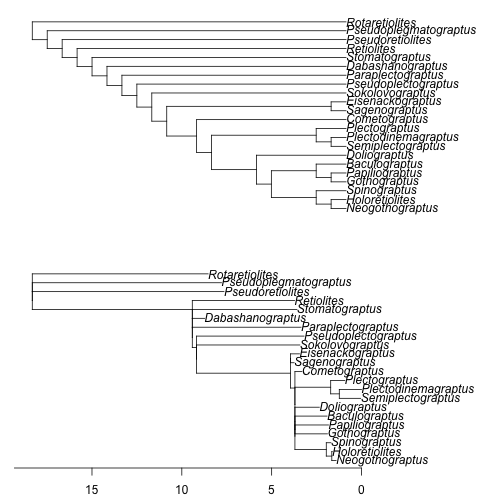
Figure 3. Randomly resolving polytomies forces a bifurcating tree, but zero-length branches remain, creating apparent polytomies. As in Figure 1, the top figure is the unscaled cladogram used as input and the lower figure is the time-scaled output, and the axis shown is time relative to the latest terminal tip. Times of observation used are the last appearance dates. Appearance dates for taxa are randomly resampled from within discrete intervals and polytomies are randomly resolved.
We get a new warning, this one telling us to beware interpreting a single output phylogeny because of the random resolution of polytomies. As discussed above, when we deal with uncertainty by using stochastic methods, like randomly resolving polytomies, it is more appropriate to generate large sample of trees for an analysis.
The plotted time-scaled phylogeny (Figure 3) will still appear to have polytomies, even though we have forced it to be dichotomous. The reason for this is the internal zero-length branches produced by having more derived taxa nested within a clade occurs earlier in the fossil record than the other members in that clade. This pushes branching nodes up against each other in the basic time-scaling method, forcing us to infer simultaneous divergence events, even though the topology is fully dichotomous.
To avoid these artifacts, we need a different time-scaling algorithm than the basic method. There are several that have been developed as just extensions of the basic time-scaling method, such as the minimum branch length method ("MBL"; Laurin, 2004), which forces nodes to shift backwards in time so that all branches meet some minimum length. To use this method in "paleotree", we need to set the type argument to mbl. Additionally, this requires setting the minimum branch length with the vartime argument. Here we will use 1 million years (1 time unit) as an example.
timetree <- bin_timePaleoPhy(tree = retioTree, timeList = retioRanges, type = "mbl", vartime = 1, randres = TRUE, add.term = TRUE, ntrees = 1, plot = TRUE)
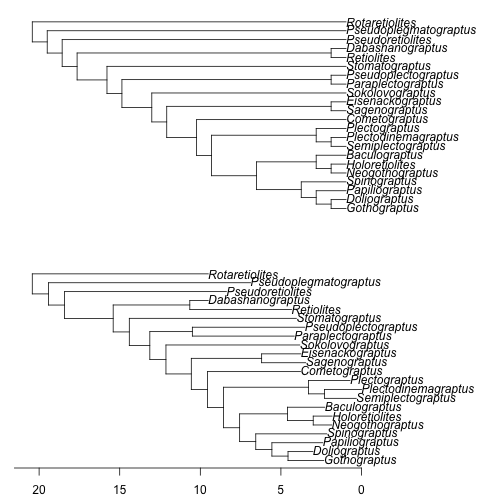
Figure 4. The Minimum Branch Length time-scaling algorithm uses the "basic" method and then adjusts divergence dates backwards in time, forcing all branches to be at least as long as some preset constant (for this example, 1 million years). As in Figure 1, the top figure is the unscaled cladogram used as input and the lower figure is the time-scaled output, and the axis shown is time relative to the latest terminal tip. Times of observation used are the last appearance dates. Appearance dates for taxa are randomly resampled from within discrete intervals and polytomies are randomly resolved.
The MBL method will add a noticeably large amount of extra branch lengths to the time-scaled phylogeny (Figure 4), effectively positing that there is much more unobserved evolutionary history across the clade. Because the tree is fairly pectinate (ladder-like), there is now a long series of nodes separated at one million-year intervals, reflecting nodes pushed apart to satisfy the minimum branch length requirement. Obviously, the choices made to time-scale a tree makes assumptions about the spacing of branching events and the amount of unobserved evolutionary history. Even if we knew exactly how much unobserved evolutionary history to expect, we would not know where to arrange it on the tree.
The cal3 time-scaling method provides a solution to this, estimating how much unobserved evolutionary history to expect and placing it stochastically across the phylogeny (Bapst, 2013). Unfortunately, when divergence dates are likely to have occurred relative to sampling events is not just a function of the sampling process, but also the processes by which new lineages branch and go extinct. Thus, cal3 requires three rates to calibrate the time-scaling, hence its name. Estimating those rates can be tricky for some fossil records, but is usually quite simple for marine invertebrate datasets, and some tools to do so can be found in"paleotree".
Glossing over several alternative options, the recommended method in "paleotree" for getting a sampling rate from discrete interval data is a maximum likelihood method developed by Foote (1997), based on the frequency distribution of stratigraphic ranges (Foote and Raup, 1996). This method is implemented in the function getSampProbDisc(), and can be applied directly to the stratigraphic range data we used for time-scaling our cladogram. This function requires that the intervals in our data are sequential and of roughly the same length, which is mostly satisfied here. This function will return a lot of output:
SPresult <- getSampProbDisc(retioRanges) SPresult
## $Title ## [1] "Analysis with 1 time bins and 0 groupings ( 0 and 0 States),with 2 parameters and 22 taxa" ## ## $parameters ## extRate sampProb Completeness ## 0.2028 0.5454 0.8673 ## ## $log.likelihood ## [1] -41.41 ## ## $AICc ## [1] 87.44 ## ## $convergence ## [1] 0 ## ## $message ## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"
Most importantly among all this output, we can evaluate whether the maximum-likelihood optimizer (the standard R optimizer optim) at work within getSampProbDisc() converged properly: if $convergence is 0, then we are probably okay. The best-fit parameters are at top, in particular, the per-genus sampling probability for each biozone zone is ~0.545. Post-analysis, users should evaluate the degree to which these parameter estimates make sense, either on first principles or by comparing them to similar published estimates, perhaps for similar groups (e.g. Foote and Sepkoski, 1999). Maximum likelihood analyses can sometimes be susceptible to inferring nonsensical parameter values depending on the topography of the likelihood surface; hence the need to also ensure that the optimizer converges.
If we have prior reasons to believe that sampling varies across a given group, we can use getSampProbDisc() to fit models with different parameters to taxa in different time-intervals or different clades. We can then use Akaike Information Criterion or other metrics (Akaike, 1973; Burnham and Anderson, 2003) to compare different models of sampling variation. The small dataset used here comprises only twenty-two genera so we may lack statistical power to adequately differentiate between more complex models. For the sake of this tutorial, we will continue with our present estimate of sampling probability.
The getSampProbDisc() analysis has only provided us with the per-interval sampling probability, but cal3 time-scaling requires that we have the instantaneous rate of sampling, i.e. the rate of sampling events occurring per lineage, per time-unit. This is mainly because other metrics of sampling, like taxonomic completeness or the per-interval probability, are partly dependent on extinction rate (Foote, 1997). To get the instantaneous rate, we need to use the function sProb2sRate(), which also requires we have the mean interval length, which we can get with a little arithmetic applied to retioRanges:
meanInt <- mean(apply(retioRanges[[1]], 1, diff)) sRate <- sProb2sRate(SPresult$parameters[2], int.length = meanInt) sRate
## [1] -0.7988
We also must calculate the rates of extinction and branching to apply the cal3 time-scaling method. A typical approach would be to estimate these separately using per-capita rates (Foote, 2000) and take the long-term mean of these rates (e.g. Roy et al., 2009). getSampProbDisc() also calculates a per-interval extinction rate, which we use for our purposes here for simplicity. Additionally, branching (origination) rates are often equal to extinction rates (or close to equal) in the fossil record (Stanley, 1979; Sepkoski, 1998), and so we will use the extinction rate estimate as the branching rate, again as a simplifying assumption for this tutorial. To get the per-lineage, per-time-unit extinction rate, we need to divide the extinction rate by the mean interval length:
extRate <- SPresult$parameters[1]/meanInt
With these three rates, we can apply the cal3 time-scaling method. As this is a discrete interval dataset, we should apply the function bin_cal3TimePaleoPhy(). By default, the cal3 time-scaling functions randomly resolve polytomies, although weighted toward solutions that match the mismatch expected under a model of sampling in the fossil record. In addition, bin_cal3TimePaleoPhy() includes the "terminal" stratigraphic ranges of taxa in the output tree by default, the exact opposite of the default behavior for bin_timePaleoPhy(), but this behavior can be changed via the arguments such as FAD.only.
timetree <- bin_cal3TimePaleoPhy(retioTree, retioRanges, brRate = extRate, extRate = extRate, sampRate = sRate, ntrees = 1, plot = TRUE)
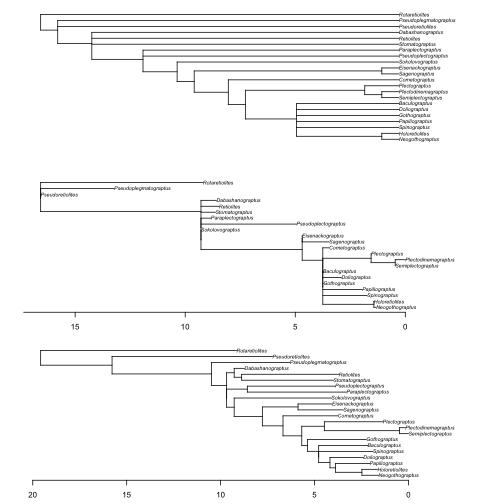
Figure 5. Branching times are stochastically resampled under a model of sampling and diversification using the cal3 time-scaling method, which accounts for ancestor-descendant relationships. Similar to Figures 1-4, the top figure is the unscaled cladogram used as input and the middle figure is that tree time-scaled using the "basic" method. The lowest figure is the tree time-scaled using the cal3 algorithm. The axes shown are time relative to the latest terminal tip in each time-scaled tree, respectively. Times of observation used are the last appearance dates. Appearance dates for taxa are randomly resampled from within discrete intervals and polytomies are resolved according to a model of expected fit to the fossil record.
Just like before, we get a number of warnings to not interpret any single time-scaled tree, particularly as cal3 is a stochastic time-scaling algorithm. The plotted time-scaled tree is shown with both the unscaled cladogram and the basic time-scaled tree, which we calculated above (Figure 5). Overall, the cal3 algorithm has not greatly shifted the nodes further back in time, because additional unsampled evolutionary history is unlikely given the high sampling rates we estimated for our graptoloid data. In particular, some of the zero length branches in the "basic" time-scaled tree have only lengthened slightly in the cal3 time-scaled phylogeny.
Generating a sample of time-scaled trees is absolutely necessary to grasp the uncertainty in an analysis using any randomizations, either singular or in combination, such as the randomizations previously discussed: cal3 time-scaling, random resolving of polytomies or random resampling of dates from discrete intervals. We can then run our analysis across the sample of trees. For instance, if we are interested in the rate of trait change, we look at the distribution of rate estimates across a sample of trees. If we want to use model-fitting analyses to test between different patterns of trait evaluation, we would evaluate Akaike weights (Burnham and Anderson, 2002) for those models across the different phylogenies. For the most part, these methods are not available in "paleotree", but can be found in other packages for R. This package does contain functions for analyzing diversity over multiple datasets that are applicable, however. The "paleotree" function multiDiv() can be used to examine the distribution of phylogenetic-corrected diversity estimates across geologic time. For example, we can easily generate a hundred trees and look at the resulting diversity curve:
timetrees <- bin_cal3TimePaleoPhy(retioTree, retioRanges, brRate = extRate, extRate = extRate, sampRate = sRate, ntrees = 100, plot = FALSE) multiDiv(timetrees)
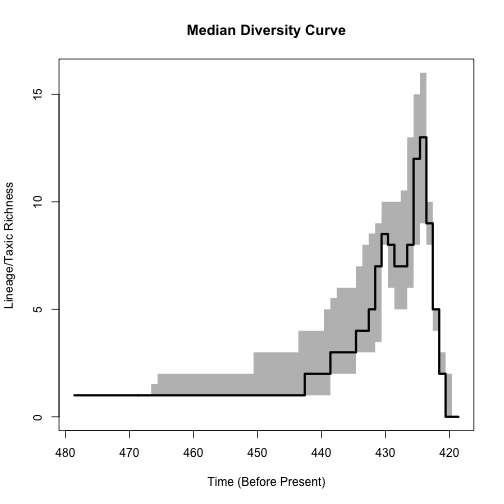
Figure 6. A median diversity curve with 95% quantiles calculated across a sample of 100 time-scaled phylogenies output using the cal3 time-scaling algorithm. The thick line is the median diversity estimated for each interval across the tree sample and the gray boxes represent the two-tailed 95% quantile for the range of diversities observed across the output trees. The phylogenies used had appearance dates randomly resampled from within intervals, polytomies resolved according to a model of expected fit to the fossil record and used last appearance dates as the times of observation.
The result (Figure 6) depicts the median lineage diversity for each interval as a thick black line, with a surrounding arrangement of gray blocks that represent the 95% quantiles for the per-interval lineage diversity, across the sample of time-scaled phylogenies.
References
- Akaike H Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Csaki F (eds) Second International Symposium on Information Theory, Akademiai Kiado, Budapest., 1973. pp 267-281.
- Bapst DW (2012) paleotree: an R package for paleontological and phylogenetic analyses of evolution. Methods in Ecology and Evolution 3 (5):803-807. doi:10.1111/j.2041-210X.2012.00223.x.
- Bapst DW (2013) A stochastic rate-calibrated method for time-scaling phylogenies of fossil taxa. Methods in Ecology and Evolution 4 (8):724-733. doi:10.1111/2041-210x.12081.
- Bates DEB, Kozlowska A, Lenz AC (2005) Silurian retiolitid graptolites: Morphology and evolution. Acta Palaeontologica Polonica 50 (4):705-720.
- Burnham KP, Anderson DR (2002) Model Selection and Mulitmodel Inference: A Practical Information-Theoretic Approach. Springer, New York.
- Foote M (1997) Estimating Taxonomic Durations and Preservation Probability. Paleobiology 23 (3):278-300.
- Foote M (2000) Origination and extinction components of taxonomic diversity: general problems. In: Erwin DH, Wing SL (eds) Deep Time: Paleobiology's Perspective. The Paleontological Society, Lawrence, Kansas, pp 74-102.
- Foote M, Raup DM (1996) Fossil preservation and the stratigraphic ranges of taxa. Paleobiology 22 (2):121-140. Laurin M (2004) The Evolution of Body Size, Cope's Rule and the Origin of Amniotes. Systematic Biology 53 (4):594-622.
- Norell MA (1992) Taxic origin and temporal diversity: the effect of phylogeny. In: Novacek MJ, Wheeler QD (eds) Extinction and phylogeny. Columbia University Press, New York, pp 89-118.
- Paradis E (2012) Analysis of Phylogenetics and Evolution with R. Springer, New York.
- Paradis E, Claude J, Strimmer K (2004) APE: Analyses of phylogenetics and evolution in R language. Bioinformatics 20 (2):289-290.
- R Core Team (2013) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
- Roy K, Hunt G, Jablonski D (2009) Phylogenetic Conservatism of Extinctions in Marine Bivalves. Science 325 (5941):733-737.
- Sadler PM, Cooper RA, Melchin M (2009) High-resolution, early Paleozoic (Ordovician-Silurian) time scales. Geological Society of America Bulletin 121 (5-6):887-906.
- Sepkoski JJ (1998) Rates of speciation in the fossil record. Philosophical Transactions: Biological Sciences 353 (1366):315-326
- Stanley SM (1979) Macroevolution: Patterns and Process. W. H. Freeman, Co., San Francisco.